CS6140 Machine Learning
HW5 - Features
Make sure you check the syllabus
for the due date. Please use the notations adopted in class, even
if the problem is stated in the book using a different notation.
SpamBase-Poluted dataset:
the same datapoints as in the original Spambase dataset, only with
a lot more columns (features) : either random values, or somewhat
loose features, or duplicated original features.
SpamBase-Poluted with missing values dataset: train,
test.
Same dataset, except some values (picked at random) have been
deleted.
Digits Dataset (Training data,
labels. Testing data,
labels): about 60,000 images, each 28x28 pixels representing
digit scans. Each image is labeled with the digit represented, one
of 10 classes: 0,1,2,...,9.
PROBLEM 1 Adaboost with bad features[50 points]
A) Spambase (original dataset) : Implement feature
analysis for Adaboost as part of your boosting code. Run
Adaboost with Decision Stumps for 300 rounds; then list the top ten
features : rank features by the fraction of average margin (of the
overall classifier) due to each feature.
Cheng's top 15 features (IDs as column number in data, starting at
0): 52, 51, 56, 15, 6, 22, 23, 4, 26, 24, 7, 54, 5, 19, 18.
B) Spambase polluted dataset
: Run Adaboost on polluted Spambase and report performance - why
does it still work? Expected Accuracy: 93%.
PROBLEM 2 PCA [50 points]
Spambase
polluted dataset.
A) Train and test Naive Bayes. Why the dramatic decrease in
performance ? Expected Accuracy with Gaussian Fits: 62%
B) Run PCA first on the dataset in order to reduce dimensionality to
about 100 features. You can use a PCA package or library of your
choice.
Then train/test Naive Bayes on the PCA features. Explain the
performance improvement. (To make it work, you have to apply PCA
consistently to training and testing points: either apply for
training and store the PCA transformation to apply it later for each
test point; or apply PCA once for entire dataset)
Expected Accuracy on Naive Bayes with Gaussian Fits, running on PCA
features: 73%.
C) Implement your own PCA, and rerun
Naive Bayes on obtained features.
D) [Optional , no credit] Run LDA instead of PCA before you
train the Naive Bayes. You can use a LDA package or library of your
choice.
PROBLEM 3 Missing Values [50 points]
A) Spambase polluted dataset with missing values: train,
test.
Run a slightly modified Naive Bayes to deal with the missing values,
as described in
notes following KMurphy 8.6.2. (Essentially runs the
independence product from Naive Bayes ignoring the factors
corresponding to missing features.)
Expected Accuracy when using Bernoulli fits: 80%.
B) [Optional no credit] Run tSNE library first on the dataset, computing distances/similarities with missing values. Then re-train and test Naive Bayes using the tSNE representations.
PPROBLEM 4 L1 Feature Selection [50 points]
Run a strongL1-regularized regression (library) on 20NG dataset 8-class version, and select 200 features (words) based on regression coefficients absolute value.
Then reconstruct the dateaset with only these selected features, and run L2-regularized classifier. Report accuracy per class.
PROBLEM 5 : Implement Kernel PCA for linear regression (Optional, no credit)
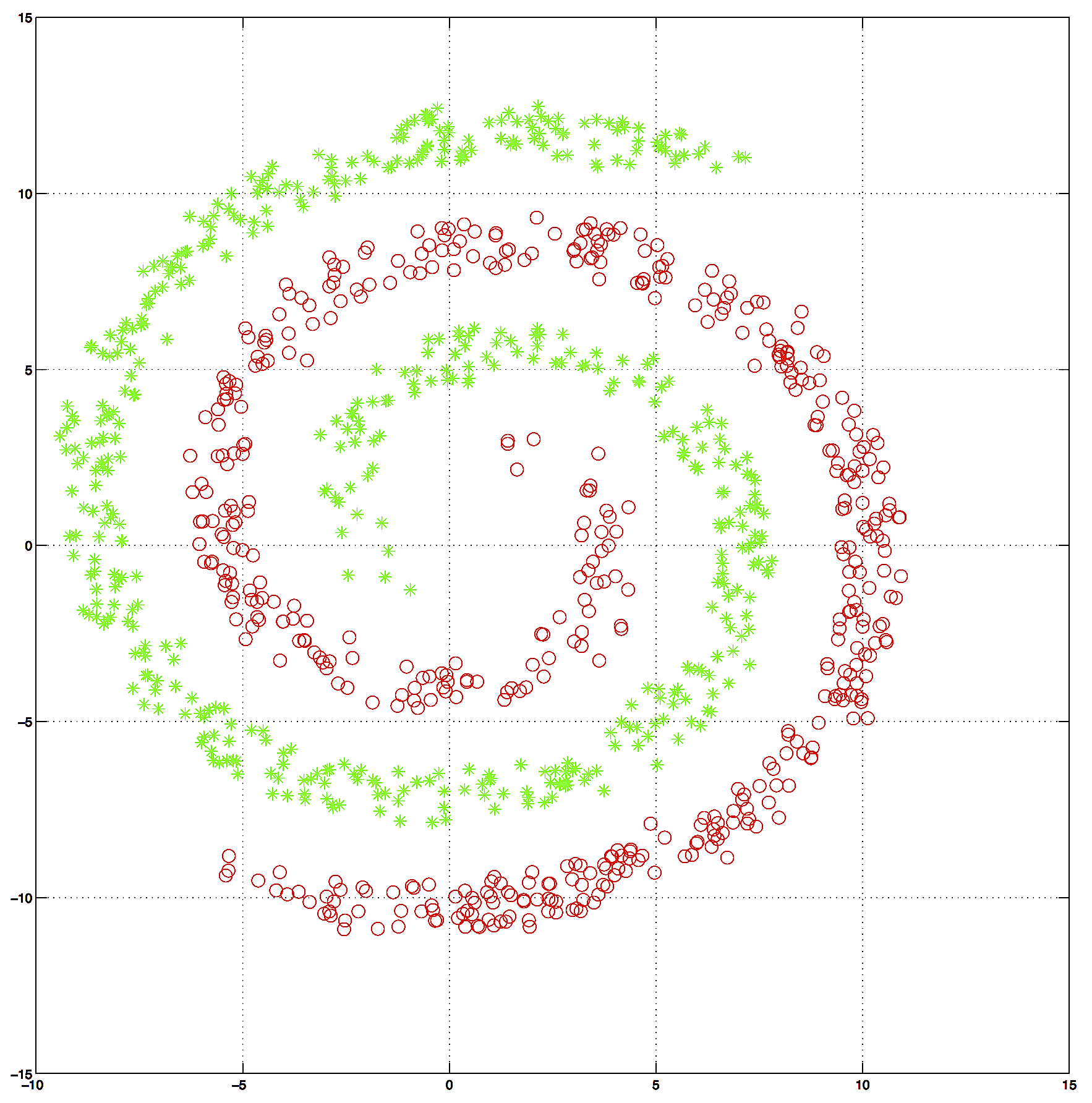
Dataset: 1000 2-dim datapoints TwoSpirals
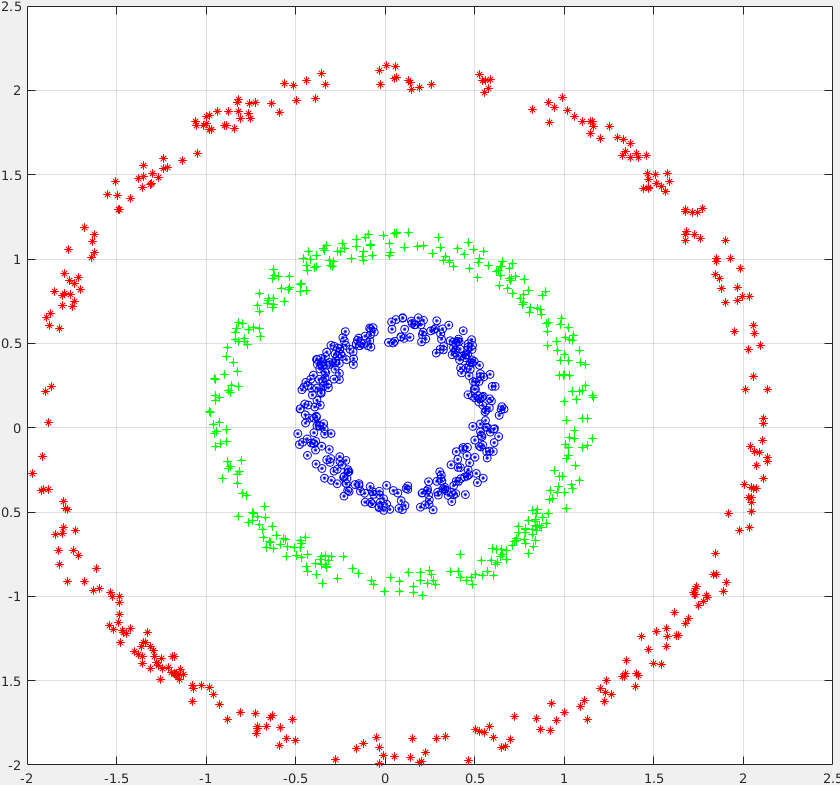
Dataset: 1000 2-dim datapoints ThreeCircles
A) First, train a Linear Regression (library) and confirm that it doesnt work , i.e. it has a high classification error or high Root Mean Squared Error.
B) Run KernelPCA with Gaussian Kernel to obtain a representation of T features. For reference these steps we demoed in class (Matlab):
%get pairwise squared euclidian distance
X2 = dot(X,X,2);
DIST_euclid = bsxfun(@plus, X2, X2') - 2 * X * X';
% get a kernel matrix NxN
sigma = 3;
K = exp(-DIST_euclid/sigma);
%normalize the Kernel to correspond to zero-mean
U = ones(N)/ N ;
Kn = K - U*K -K*U + U*K*U ;
% obtain kernel eignevalues, vectors; then sort them with largest eig first
[V,D] = eig(Kn,'vector') ;
[D,sorteig] = sort(D,'descend') ;
V = V(:, sorteig);
% get the projection matrix
XG = Kn*V';
%get first 3 dimmensions
X3G = XG(:,1:3);
%get first 20 dimmensions
X20G = XG(:,1:20);
%get first 100 dimmensions
X100G = XG(:,1:100);
C) Retrain Linear regression on the transformed D-dim data. How large D needs to be to get good performance?
PROBLEM 6 Image Feature Extraction [GR ONLY]
Mnist Digit Dataset or
Mnist (plain text) Digit Dataset
Implement and run HAAR feature Extraction for each image on the
Digit Dataset. Then train and test a 10-class ECOC-Boosting on the
extracted features and report performance. You can sample the
training set (say 20% of each class), in order to scale down the
computation.
Expected Accuracy when using 200 HAAR features, 50 random ECOC,
each Adaboost trained for 200 rounds: 89%.
(Hint: For extracting the MNIST dataset, here are example code
for
Python,
MATLAB
Java
)
HAAR features for Digits Dataset :First randomly
select/generate 100 rectangles fitting inside 28x28 image box. A
good idea (not mandatory) is to make rectangle be constrained to
have approx 130-170 area, which implies each side should be at
least 5. The set of rectangles is fixed for all images. For each
image, extract two HAAR features per rectangle (total 200
features):

- the black horizontal difference black(left-half) -
black(right-half)
- the black vertical difference black(top-half) -
black(bottom-half)
You will need to implement efficiently a method to compute the black
amount (number of pixels) in a rectangle, essentially a procedure
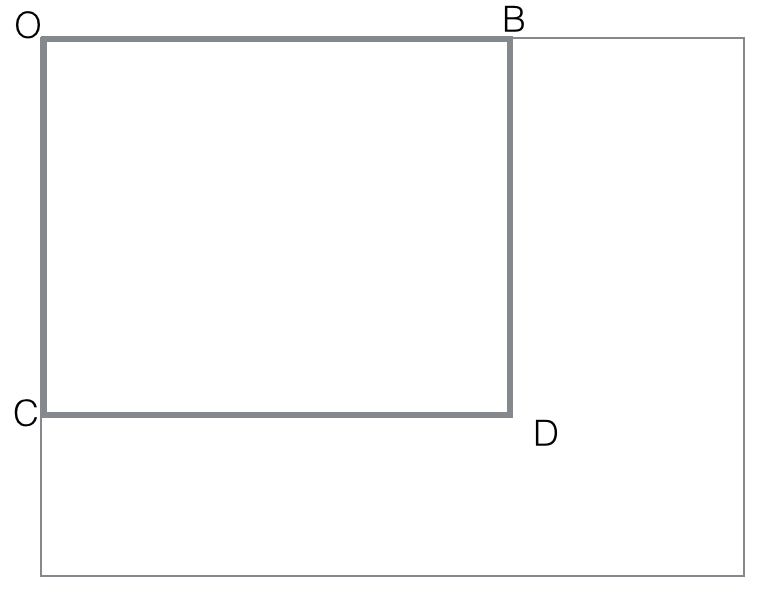
black(rectangle). Make sure you follow the idea presented in notes :
first compute all black (rectangle OBCD) with O fixed corner of an
image. These O-cornered rectangles can be computed efficiently with
dynamic programming
black(rectangle OBCD)=
black(rectangle-diag(OD))
= count of black points in OBCD matrix
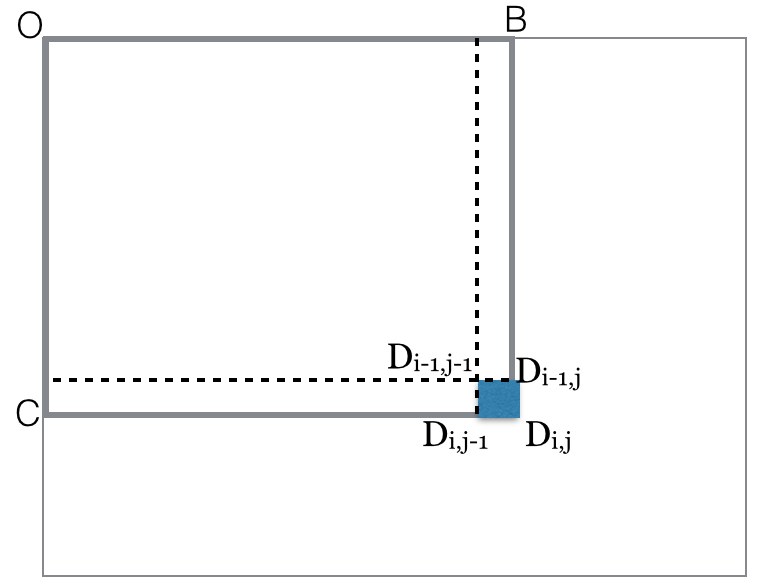
for i=rows
for j=columns
black(rectangle-diag(ODij)) = black(rectangle-diag(ODi,j-1))
+ black(rectangle-diag(ODi-1,j))
- black(rectangle-diag(ODi-1,j-1))
+ black(pixel Dij)
end for
end for
Assuming all such rectangles cornered at O have their black computed
and stored, the procedure for general rectangles is quite easy:
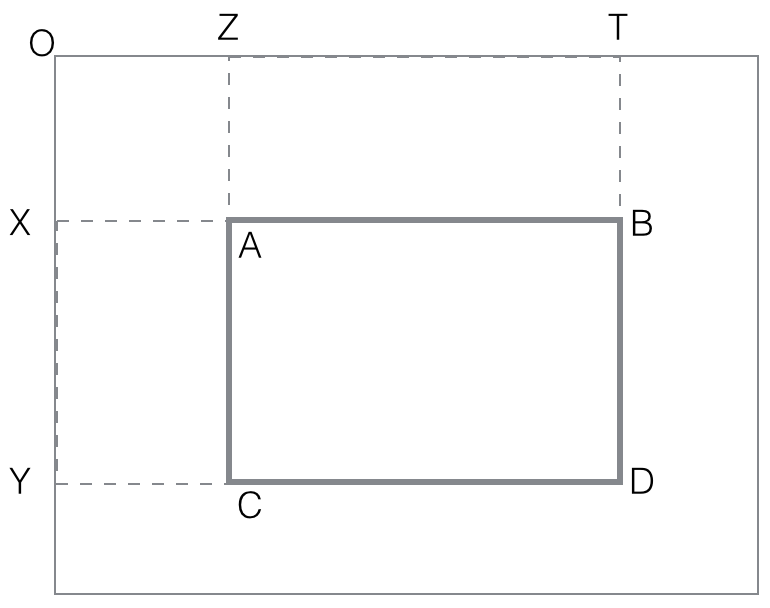
black(rectangle ABCD) =
black(OTYD) - black(OTXB) - black(OZYC) + black(OZXA)
The last step is to compute the two feature (horizontal, vertical)
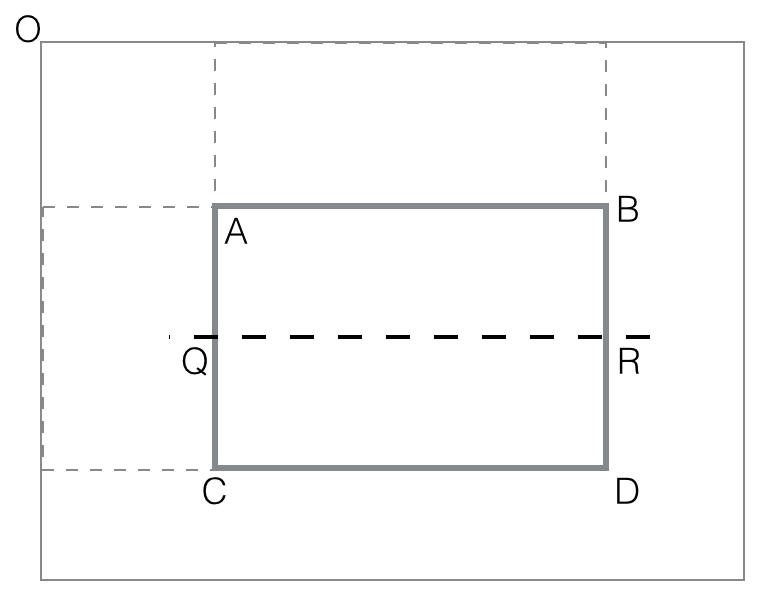
values as differences:
vertical_feature_value(rectangle ABCD) = black(ABQR) -
black(QRCD)
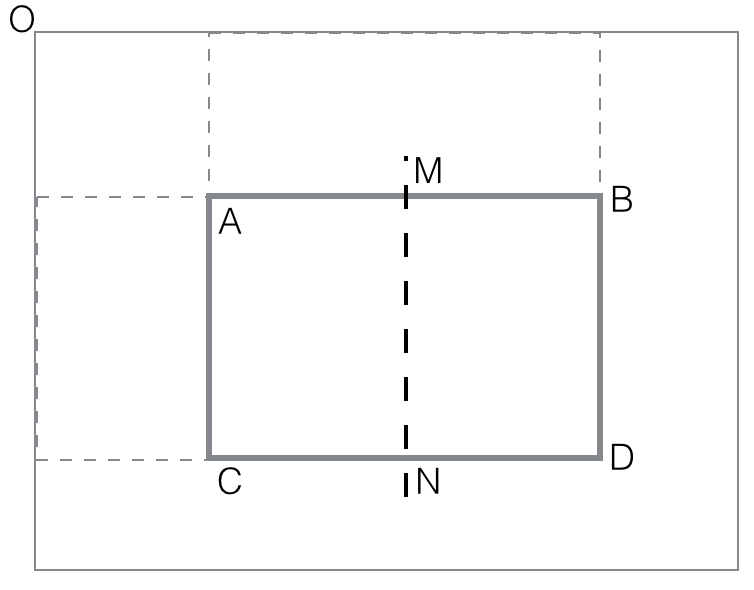
horizontal_feature_value(rectangle
ABCD) = black(AMCN) - black(MBND)
PROBLEM 7 [Optional, no credit] Regularized Regression for noise data
A) Spambase polluted dataset
run Logistic Regression for classification. Expected Accuracy: 85%
B) Run Regularized Regression (separate runs for LASSO and RIDGE)
using a package for regularization. For example use the scikit-learn
(Python) or Liblinear (C++) implementation of LASSO. Compare with
Logistic Regression performance. Expected Accuracy of Lasso Logistic
Regression: 93%.
C) Implement your own RIDGE optimization for Logistic Regression.
Expected Accuracy of Ridge Logistic Regression: 92%.
D) Implement your own LASSO
optimization for linear regression.
PROBLEM 7 Boosting with Dynamic Features [Optional, no credit]
A) Run Boosting (Adaboost or Rankboost or Gradient Boosting) to
text documents from 20 Newsgroups without extracting features in
advance. Extract features for each round of boosting based on
current boosting weights.
B) Run Boosting (Adaboost or Rankboost or Gradient Boosting) to
image datapoints from Digit Dataset without extracting features in
advance. Extract features for each round of boosting based on
current boosting weights. You can follow this paper.







