CS6140 Machine Learning
HW2 - Gradient Descent Learning
Make sure you check the syllabus for the due date. Please
use the notations adopted in class, even if the problem is stated
in the book using a different notation.
Make sure to read the notes on Gradient Descent for Regression,
and chapter 5 of DHS, up to (including 5.6 Relaxation Procedures)
PROBLEM 1 [50 points]
A) Run Linear Regression regularized (Ridge) with normal equations.
B) Train Linear Regression using Gradient Descent (and then test) on
Spambase and Housing datasets form HW1.
C) Run Gradient Descent Logistic Regression on Spambase data.
Note: Normalization matters. When you
normalize data features (one feature at a time), you need to
normalize all data (train, test, validation) together, as opposed
to normalize separately training and testing sets.
Compare for each dataset training and testing performance across all
four learning algorithms by making a table like below
|
Decision or Regression Tree
|
Linear Regression (Normal Equations)
|
Linear Ridge Regression (Normal Equations)
|
Linear Regression(Gradient Descent)
|
LogisticRegression(Gradeint Descent)
|
Spambase
|
Train ACC:
Test ACC:
|
Train ACC:
Test ACC: |
Train ACC:
Test ACC: |
Train ACC:
Test ACC: |
Train ACC:
Test ACC: |
Housing
|
Train MSE:
Test MSE: |
Train MSE:
Test MSE: |
Train MSE:
Test MSE: |
Train MSE:
Test MSE: |
N/A . - WHY?
|
C) For classification (Spambase), produce Confusion Matrices
(TruePos, FalsePos, TrueNeg, FalseNeg) for Decision
Trees, Linear Regression and Logistic Regression - three 2x2
matrices. You will have to use a fixed threshold for each
regression algorithm.
D) For classification (Spambase), produce ROC plots comparison
between linear regression and logistic regression - two curves.
Compute the AUC for each curve.
PROBLEM 2 [40 points] Perceptron Algorithm (Gradient Descent for
a different objective)
Step 1: Dowload the perceptron learning data set that I have created.
The data set is tab delimited with 5 fields, where the first 4
fields are feature values and the last field is the {+1,-1} label;
there are 1,000 total data points.
Step 2: Create a perceptron learning algorithm, as described in
class.
Step 3: Run your perceptron learning algorithm on the data set
provided. Keep track of how many iterations you perform until
convergence, as well as how many total updates (corresponding to
mistakes) that occur through each iteration. After convergence, your
code should output the raw weights, as well as the normalized
weights corresponding to the linear classifier
w1 x1 + w2 x2 + w3 x3 + w4 x4 = 1
(You will create the normalized weights by dividing your perceptron
weights w1, w2, w3, and w4 by -w0, the weight corresponding to the
special "offset" feature.)
Step 4: Output the result of your perceptron learning algorithm as
described above. Your output should look something like the
following:
[jaa@jaa-laptop Perceptron]$ perceptron.pl perceptronData.txt
Iteration
1 , total_mistake 136
Iteration 2 , total_mistake 68
Iteration 3 , total_mistake 50
Iteration 4 , total_mistake 22
Iteration 5 , total_mistake 21
Iteration 6 , total_mistake 34
Iteration 7 , total_mistake 25
Iteration 8 , total_mistake 0
Classifier weights: -17 1.62036704608359 3.27065807088159
4.63999040888332 6.79421449422058 8.26056991916346 9.36697370729981
Normalized with threshold: 0.0953157085931524 0.192391651228329
0.272940612287254 0.399659676130622 0.485915877597851
0.550998453370577
(Note: The output above corresponds to running on a different data
set than yours which has six dimensions as opposed to four. Your
results will be different, but you should convey the same
information as above.)
PROBLEM 3 [70 points] AUTOENCODER Neural Network
Consider the following neural network (left graph), with 8 input
units (for data with 8 features), 3 hidden units and 8 output
units, and assume the nonlinear functions are all sigmoid.
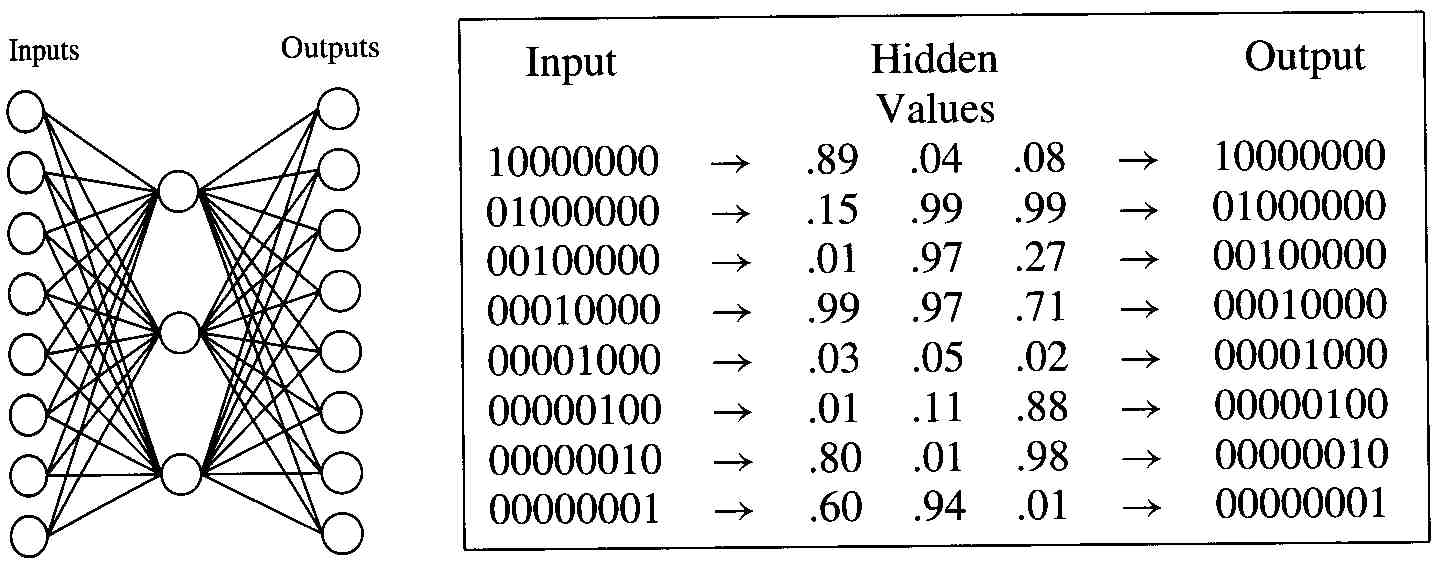
a)The 8 training data inputs are identical with the outputs, as
shown in the right side table. Implement this network and the
backpropagation algorithm to compute all the network weights; you
should initialize the weights with nontrivial values (i.e not
values that already minimize the erorr).
HINT: on the trained network, you should obtain values for the
hidden units somehow similar with the ones shown in the table (up
to symmetry). Feel free to make changes to the algorithm that suit
your implementation, but briefly document them.
b) Since the outputs and inputs are identical for each datapoint,
one can view this network as an encoder-decoder mechanism. (this
is one of the uses of neural networks). In this context, explain
the purpose of the training algorithm. (I expect a rather
nontechnical --but documented-- answer).
c) Can this encoder-decoder scheme work with 1 hidden unit? Can
it work with 2 hidden units? What if there are more than 8 inputs
and outputs? Justify your answers mathematically.
Hints: Some students worked easier from this algorithm,
rather than the one from Mitchell's
book
PROBLEM 4 [20 points]
DHS ch6, Pb1
Show that if the transfer function of the hidden units is linear, a
three-layer network is equivalent to a two-layer one. Explain why,
therefore, that a three-layer network with linear hidden units
cannot solve a non-linearly separable problem such as XOR or n-bit
parity.
PROBLEM 5 [30 points]
Read prof Andrew Ng's lecture on ML
practice advice. Write a brief summary (1 page) explaining
the quantities in the lecture and the advice.
Read prof Pedro Domingos's paper on A
Few Useful Things to Know about Machine Learning. Write a
brief summary (1 page), with bullet points.
PROBLEM 6 [Extra Credit]
DHS chapter 5 Pb 2 (page 271)
PROBLEM 7 [Extra Credit]
DHS chapter 5 Pb 5, page 271
PROBLEM 8 [Extra Credit]
DHS chapter 5 Pb 6, page 271
PROBLEM 9 [extra credit]
For a function f(x1,x2,..., xn) with real values, the "Hessian"
is the matrix of partial second derivatives

Consider the log-likelihood function for logistic regression
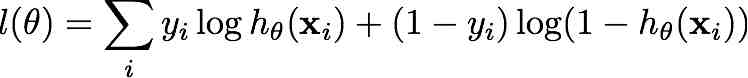
Show that its Hessian matrix H is negative semidefinite, i.e. for
any vector z satisfies
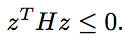
Remark: This fact is sometimes written
and implies the log-likelihood function
is concave.
Hint: 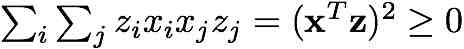
PROBLEM 10 [extra credit]
Run Logistic Regression on the Spambase dataset, but using Newton's
numerical method instead of Gradient Descent. An intro to Newton's
method can be found in the lecture notes.
PROBLEM 11 [extra credit]
Given a ranking of binary items by prediction score, the ROC is the
curve plotted of True Positives vs False Positives for all possible
thresholds. The AUC is the area under the ROC curve.
Prove that the AUC is also the percentage of item pairs (i,j) in
correct order.
As an illustrative example, the classifier output might be
-------------------------------------------
object score
truelabel
-------------------------------------------
A 100
1
B
99 1
C
96 0
D
95 1
E
90 1
F
85 0
G
82 1
H
60 0
K
40 0
I
38 0
The ROC curve is obtained by truncating the list above at all ranks,
and for each such threshold computing false-positive-rate and
true-positive-rate (and plot them).
The problem asks to show that the area under the ROC curve is
approximated by the percentage of pairs in correct order. In this
example the item pairs in incorrect order are (C,D), (C,E),
(C,G), (F,G)



![]()
![]()