CS6140 Machine Learning
HW1 Linear Regression, Regularization, Perceptron
Make sure you check the syllabus for the due date. Please
use the notations adopted in class, even if the problem is stated
in the book using a different notation.
We are not looking for very long answers (if you find yourself
writing more than one or two pages of typed text per problem, you
are probably on the wrong track). Try to be concise; also keep in
mind that good ideas and explanations matter more than exact
details.
DATASET 1: Housing data, training and testing sets (description). The last
column are the labels.
DATATSET 2: Spambase
dataset available from the UCI Machine
Learning Repository.
You can try to normalize each column (feature) separately with
wither one of the following ideas. Do not normalize labels.
- Shift-and-scale normalization: subtract the minimum, then
divide by new maximum. Now all values are between 0-1
- Zero mean, unit variance : subtract the mean, divide by the
appropriate value to get variance=1.
- When normalizing a column (feature), make sure to normalize
its values across all datapoints (train, test, validation, etc)
The Housing dataset comes with predefined training and testing
sets. For the Spambase dataset use K-fold cross-validation :
- split into K folds
- run your algorithm K times each time training on K-1 of them
and testing on the remaining one
- average the error across the K runs.
20Newsgroup dataset dataset.Or you can download 20NewsGroup from scikit-learn
For most problems better use 20Newsgroup_8classes dataset with extracted features (The zip file is called
8newsgroup.zip because the 20 labels have been grouped into 8 classes to make the problem easier).
PROBLEM 1 [30 points]
A) Using each of the two datasets above, apply regression on the
training set to find a linear fit with the labels. Implement
linear algebra exact solution (normal equations).
- Compare the training and testing errors
- for Housing (quantitative labels) : use mean sum of square differences between prediction and actual label.
- for Spambase : use a threshold (your choice) for prediction, then measure train/test accuracy
B) Train/test Linear Regression L2-regularized (Ridge) with normal equations.
PROBLEM 2 [30 points]
A) Train/test L1-regularized Linear Regression on Housing data. Use the scikit-learn library call; appropriately set input params. Try different values of L1 penalty, and create a plot (X_axis=L1 value; y_axis=test performance)
B) Run a strongL1-regularized regression (library) on 20NG dataset 8-class version, and select 200 features (words) based on regression coefficients absolute value.
Then reconstruct the dateaset with only these selected features, and run L2-regularized classifier (library). Report accuracy per class.
PROBLEM 3 [30 points]
Derive explicit formulas for normal equations solution
presented in class for the case of one input dimension.
(Essentially assume the data is (x_i,y_i) i=1,2,..., m and you
are looking for h(x) = ax+b that realizes the minimum mean square
error. The problem asks you to write down explicit formulas for a
and b.)
HINT: Do not simply copy the formulas from here
(but do read the article): either take the general formula derived
in class and make the calculations (inverse, multiplications,
transpose) for one dimension or derive the formulas for a and b
from scratch; in either case show the derivations. You can compare
your end formulas with the ones linked above.
PROBLEM 4 [30 points, GR ONLY]
DHS chapter5,
The convex hull of a set of vectors xi,i = 1,...,n is the set of all
vectors of the form
where the coefficients αi are nonnegative and sum to one. Given two
sets of vectors, show that either they are linearly separable or
their convex hulls intersect.
Hint on easy part: that the two conditions cannot happen
simultaneously. Suppose that both statements are true, and consider
the classification of a point in the intersection of the convex
hulls.
[Optional, no credit; difficult] Hard part: that at least one of the two
conditions must hold. Suppose that the convex hulls dont intersect;
then show the points are linearly separable.
PROBLEM 5 [30 points]
Read prof Andrew Ng's lecture on ML
practice advice. Write a brief summary (1 page) explaining
the quantities in the lecture and the advice.
Read prof Pedro Domingos's paper on A
Few Useful Things to Know about Machine Learning. Write a
brief summary (1 page), with bullet points.
PROBLEM 6 [30 points] Perceptron Algorithm (Gradient Descent for
a different objective)
Step 1: Download the perceptron learning data set that I have created.
The data set is tab delimited with 5 fields, where the first 4
fields are feature values and the last field is the {+1,-1} label;
there are 1,000 total data points.
Step 2: Create a perceptron learning algorithm, as described in
class.
Step 3: Run your perceptron learning algorithm on the data set
provided. Keep track of how many iterations you perform until
convergence, as well as how many total updates (corresponding to
mistakes) that occur through each iteration. After convergence, your
code should output the raw weights, as well as the normalized
weights corresponding to the linear classifier
w1 x1 + w2 x2 + w3 x3 + w4 x4 = 1
(You will create the normalized weights by dividing your perceptron
weights w1, w2, w3, and w4 by -w0, the weight corresponding to the
special "offset" feature.)
Step 4: Output the result of your perceptron learning algorithm as
described above. Your output should look something like the
following:
[jaa@jaa-laptop Perceptron]$ perceptron.pl perceptronData.txt
Iteration
1 , total_mistake 136
Iteration 2 , total_mistake 68
Iteration 3 , total_mistake 50
Iteration 4 , total_mistake 22
Iteration 5 , total_mistake 21
Iteration 6 , total_mistake 34
Iteration 7 , total_mistake 25
Iteration 8 , total_mistake 0
Classifier weights: -17 1.62036704608359 3.27065807088159
4.63999040888332 6.79421449422058 8.26056991916346 9.36697370729981
Normalized with threshold: 0.0953157085931524 0.192391651228329
0.272940612287254 0.399659676130622 0.485915877597851
0.550998453370577
(Note: The output above corresponds to running on a different data
set than yours which has six dimensions as opposed to four. Your
results will be different, but you should convey the same
information as above.)
PROBLEM 7 [Optional, no credit; read DHS ch5]
DHS chapter5
A classifier is said to be a piecewise linear machine if its
discriminant functions have the form
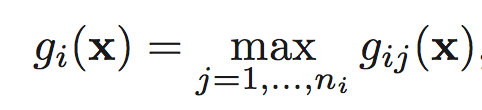
where
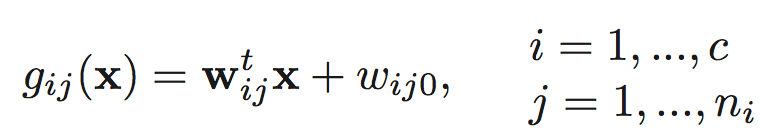
(a) Indicate how a piecewise linear machine can be viewed in terms
of a linear machine for classifying subclasses of patterns.
(b) Show that the decision regions of a piecewise linear machine can
be non convex and even multiply connected.
(c) Sketch a plot of gij(x) for a one-dimensional example in which
n1 = 2 and n2 = 1 to illustrate your answer to part (b)
PROBLEM 8 [Optional, no credit]
With the notation used in class (and notes), prove that
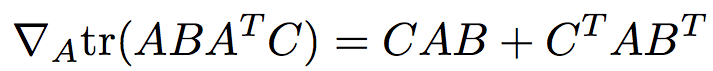
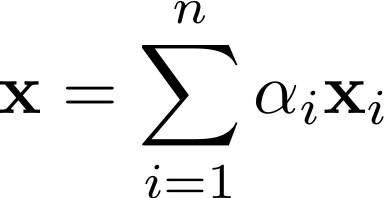
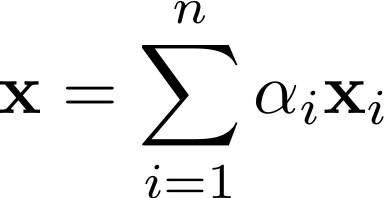
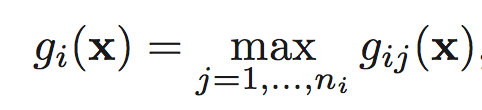
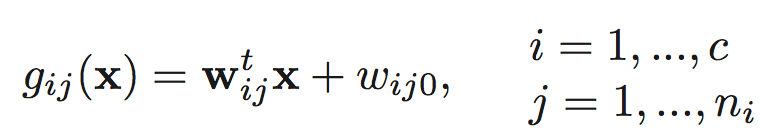
![]()