- 1.
- On a square sheet of graph paper ( with
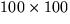 little squares ) I have drawn several rectangles. Each rectangle
consist of entire little squares of the grid, different rectangles
never overlap or touch each other (see Fig. 2).
little squares ) I have drawn several rectangles. Each rectangle
consist of entire little squares of the grid, different rectangles
never overlap or touch each other (see Fig. 2).
Given the array A[100][100] in which an entry A[i][j] = 1 if
the square (i, j) of the grid belongs to one of the rectangles,
and A[i][j] = 0 otherwise. Write a program that counts the
number of rectangles. (Think of this as the easiest problem
related to "computer vision".)
- 2.
- Print out in the increasing order all simple fractions between
and 1 such that their denominators are no greater than 7.
Example: 3/6 should not be printed, because, although its
denominator is less than 7, it is not simple and can be further
simplified, 3/ 6 = 1/2.
- 3.
- Given an array of positive integers A[N] and an integer M . It is known that
the sum of several elements of the array is equal to M . Neither their
positions nor their number are known. Find them.
Notes: 1. Notice that the elements need not be consequtive. For instance,
for
![A[8] = { 3, 8, 31, 25, 4, 15, 5, 21 }](img12.gif)
and M = 17 we have
8+4+5 = 17.
2. You may want to solve a simplified version of the problem,
assume first that the number of desired elements is also given
(say, 3, as in the above example).
3. Try to solve the problem without the condition that all inetgers in the array are positive.
- 4.
- Given an inetger array A[N] of length N. Rearrange
its entries so that all the non-zero entries are in the beginning
of the array (and their original relative order is preserved), and
all the zeros are at the and of the array. You are not allowed
to use another array.
- 5.
- Given a two-dimensional arrray A[M][N]. We call an entry
of the array a saddle point if it is both the smallest
one in its row and the largest one in its column. Output
the indices of a saddle point of A or signal failure if no
such entry exists.
- 6.
- Given two integer arrays X[N] and Y[M], N > M.
Write a program that determines if the first array X[N]contains
a subsequence of M entries same as those of Y[M], in the same
order and outputs either 'yes' or 'no'.
![]()