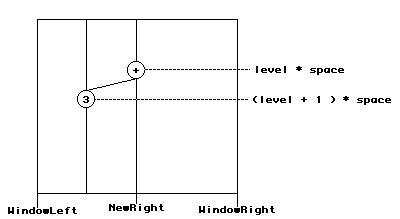
Make sure to increment level when you make your recursive calls in
Objectives
See how binary trees are related to arithmetic or algebraic expressions.
Write a program to:
We usually write the expression 5 + 2 to represent the sum of the numbers 5 and 2.
This is called the infix
form of the expression. The same sum can be represented by the prefix
form + 5 2. One advantage of the prefix form is that parenthesis are never needed.
| The infix expression: | is represented in prefix notation by: |
| (301 + 42) * 56 | * + 301 42 56 |
Overview
Your first task will be to write a Constructor to build a tree from a prefix expression.
As the destructor is supplied and writes out the nodes it is deleting, you should
be able to tell whether your Constructor is working.
Next, you will write a recursive member function to evaluate an expression tree or
give error messages when the tree is incomplete or the string is too long.
Finally, a recursive
member function to draw the tree. This is different than the way the drawing of
a binary tree was implemented in the Binary Search Tree Lab. This time we do not
have node numbers, but pass some geometric information about the drawing region.
You will also make your tree-drawing routine give feedback when the tree is incomplete or there
is non-digit data at a leaf.
Part 1: Building an Expression Tree
Start by running the application ExpTrees.
Try some simple strings:
| Valid Strings: | Invalid Strings: |
| +34 | + |
| +3*56 | +3 |
| +*356 | 345 |
**-94*+352-84 +/34-5 *+26-3+47+59 ++++ab+36+cd+7e
Now, look at the code in ExpTrees.h file.
It starts with two functions that are external to the class Tree.
You will use these functions IsOperator(ch) and IsDigit(ch) to examine the characters in the input string.
Exercise 2:
Next comes the skeleton of the definition of the class Tree and its member struct Node. Read through this file carefully. The destructor and some simple constructors
are supplied. Your first coding task is to implement the fourth constructor Tree::Node::Node(char*& s). Put this implementation (and the others in this lab) in the ExpTrees.cp
file.
Be careful. This is the hardest part of the lab. Here are some tips:
Exercise 3:
Write the member function Tree::Node::Eval(double& Val).
Exercise 4:
Implement the member function
void Tree::Node::Draw(int WindowLeft, int WindowRight , int level)
This is a preorder recursive function. Draw the Node then draw the left and right subtrees. Look at the DrawNode and DrawLink Functions. You don't have to worry about their implementations which are supplied
but you do have to understand what they do.
void DrawNode(int WindowLeft, int WindowRight, int level, char data, bool wrong);
Draws a node centered horizontally, half way between WindowLeft
and WindowRight. The vertical coordinate is computed from the level. The data is written in the node and the Boolean wrong determine whether the node is drawn in pink or blinked and then drawn in gray.

Make sure to increment level when you make your recursive calls in
void Tree::Node::Draw(int WindowLeft, int WindowRight , int level).
When you make a call to draw the left
subtree, the new WindowRight
will be the middle of the current window, (WindowLeft + WindowRight)/2.
void DrawLink(int WindowLeft, int WindowRight,
int level, bool Left);
draws a link (line segment) from the bottom of the node centered at (WindowLeft + WindowRight)/2. to the top of its left child if the BooleanLeft is true and to its right child if Left is false.
Extra Credit:
Last Updated: May 11, 1997 10:41 am by