CS6200/IS4200: Information Retrieval

Homework 2

Return to basic course information.

Assigned: Friday, 27 September 2019
Due: Friday, 11 October 2019, 11:59 p.m.

PageRank

In this assignment, you will compute PageRank on a collection of 469,235 web sites.

Consider the version of PageRank described in class. PageRank can be computed iteratively as shown in the following pseudocode:

// P is the set of all pages; |P| = N
// S is the set of sink nodes, i.e., pages that have no out links
// M(p) is the set (without duplicates) of pages that link to page p
// L(q) is the number of out-links (without duplicates) from page q
// d is the PageRank damping/teleportation factor; use d = 0.85 as a fairly typical value

foreach page p in P
  PR(p) = 1/N                          /* initial value */

while PageRank has not converged do
  sinkPR = 0
  foreach page p in S                  /* calculate total sink PR */
    sinkPR += PR(p)
  foreach page p in P
    newPR(p) = (1-d)/N                 /* teleportation */
    newPR(p) += d*sinkPR/N             /* spread remaining sink PR evenly */
    foreach page q in M(p)             /* pages pointing to p */
      newPR(p) += d*PR(q)/L(q)         /* add share of PageRank from in-links */
  foreach page p
    PR(p) = newPR(p)

return PR

In order to facilitate the computation of PageRank using the above pseudocode, we would normally preprocess a document collection into a link graph, i.e., a set of records recording when document p links to document q.

Consider the following directed graph:

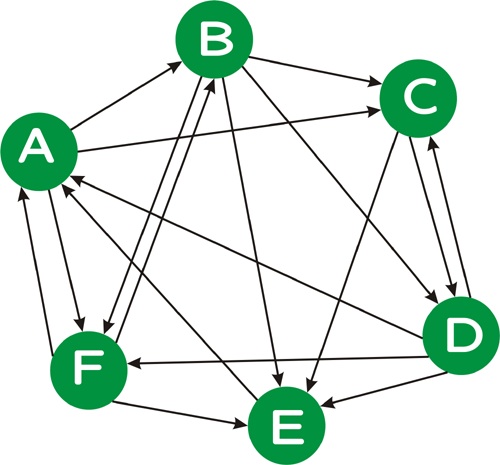
We can represent this graph as a collection of nodes, here, ordered pairs of node index and node name:

  0 A
  1 B
  2 C
  3 D
  4 E
  5 F

  0 1
  0 2
  0 5
  1 2
  1 3
  1 4
  1 5
  2 3
  2 4
  3 0
  3 2
  3 4
  3 5
  4 0
  5 0
  5 1
  5 4

Instructions

• [10 points] Implement the iterative PageRank algorithm as described above. Test your code on the six-node example using the input representation given above. Be sure that your code handles pages that have no in-links or out-links properly. (You may wish to test on a few such examples.) In later parts of this assignment, your task will be easier if you don't require loading the entire link graph into memory.

  Please hand in: a list of the PageRank values you obtain for each of the six vertices after 1, 10, and 100 iterations of the PageRank algorithm. You should have three values on each line: node id, node name, and PageRank value.

• [20 points] Download this list of .edu web sites and this list of links among them derived from the Common Crawl open-source web crawl. For the sake of brevity, the data record links among websites, not web pages. The formats for node and link data are the same as the toy example above.

  Run your iterative version of PageRank algorithm until your PageRank values "converge". To test for convergence, calculate the perplexity of the PageRank distribution, where perplexity is simply 2 raised to the (Shannon) entropy of the PageRank distribution, i.e., 2^H(PR). Perplexity is a measure of how "skewed" a distribution is: the more "skewed" (i.e., less uniform) a distribution is, the lower its preplexity. Informally, you can think of perplexity as measuring the number of elements that have a "reasonably large" probability weight; technically, the perplexity of a distribution with entropy h is the number of elements n such that a uniform distribution over n elements would also have entropy h. (Hence, both distributions would be equally "unpredictable".)

  Run your iterative PageRank algorthm, outputting the perplexity of your PageRank distibution until the change in perplexity is less than 1 for at least four consecutive iterations.

  One hint is that in this dataset, some documents with high in-link count and high PageRank are the same, so don't worry that it's a bug.

  Please hand in: a list of the perplexity values you obtain in each round until convergence as described above.

• [20 points] Sort the collection of web pages by the PageRank values you obtain.

  Please hand in:

  • a list of the document ID, website domain name, and PageRank of the top 50 websites as sorted by PageRank;
  • a list of the document ID, website domain name, and in-link count of the top 50 websites by in-link count;
  • the proportion of websites with no in-links (sources);
  • the proportion of websites with no out-links (sinks); and
  • the proportion of websites whose PageRank is less than their initial, uniform values.

Final requests

In addition to the written items mentioned above, you should hand in a copy of your source code, which should hopefully be relatively short, and instructions on (compiling and) running it. The only input to your code should be the files in the vertex and edge formats described above. The output should be a list of node IDs, website names, and their PageRank values.